Plasmacyl

This example is compatible with 1.0.6dev (22 February 2017).

The next example simulation is a modification of the plasmacyl test problem (tests/plasmacyl.cpp in the IBSimu distribution). In this problem we are extracting a 60 mA/cm2 He+ beam from plasma. Let's first build a source file plasmacyl.cpp and add the necessary header files:

#include "epot_bicgstabsolver.hpp"
#include "epot_problem.hpp"
#include "particledatabase.hpp"
#include "geometry.hpp"
#include "func_solid.hpp"
#include "epot_efield.hpp"
#include "meshvectorfield.hpp"
#include "ibsimu.hpp"
#include "error.hpp"
#include "particlediagplotter.hpp"
#include "geomplotter.hpp"
#include "config.hpp"

#ifdef GTK3
#include "gtkplotter.hpp"
#endif

The gtkplotter.hpp file is included only conditionally if GTK3 support was compiled in the IBSimu library.

The main function is pretty much the same as with the previous example. The only difference is that we need to pass the argc and argv parameters to the simulation function simu() to be able to use the interactive plotter:

int main( int argc, char **argv )
{
    try {
        ibsimu.set_message_threshold( MSG_VERBOSE, 1 );
        ibsimu.set_thread_count( 4 );
        simu( &argc, &argv );
    } catch ( Error e ) {
	e.print_error_message( ibsimu.message( 0 ) );
        exit( 1 );
    }

    return( 0 );
}

The geometry defining functions are needed for two electrodes in the problem:

bool solid1( double x, double y, double z )
{
    return( x <= 0.00187 && y >= 0.00054 && y >= 2.28*x - 0.0010 &&
            (x >= 0.00054 || y >= 0.0015) );
}


bool solid2( double x, double y, double z )
{
    return( x >= 0.0095 && y >= 0.0023333 && y >= 0.01283 - x );
}

And the simulation function itself is defined as:

void simu( int *argc, char ***argv )

The simulation geometry is 12x7 mm in size and we choose a mesh size of 0.05 mm, which is enough to model all the necessary details of the system. In this case the geometry has a cylindrical symmetry (round holes in electrodes). Therefore the boundary 3 isn't actually Neumann boundary, but a special non-existent boundary at radius zero. It is still marked as Neumann as Dirichlet boundary would force the axis to fixed potential (infinitely thin wire in the center). The first boundary is the plasma of ion source. That surface should be set to use the Neumann boundary condition. Even if the simulation should work in principle if you put the ion source to non-zero potential, I will still recommend always redefining the electrode potentials so that the ion source is at zero potential. In this way the calculation of the plasma is most accurate and minimal amount of roundoff errors happens with the floating point operations of the plasma calculation exponentials. The geometry definition:

Geometry geom( MODE_CYL, Int3D(241,141,1), Vec3D(0,0,0), 0.00005 );
Solid *s1 = new FuncSolid( solid1 );
geom.set_solid( 7, s1 );
Solid *s2 = new FuncSolid( solid2 );
geom.set_solid( 8, s2 );
geom.set_boundary( 1, Bound(BOUND_NEUMANN,     0.0 ) );
geom.set_boundary( 2, Bound(BOUND_DIRICHLET, -12.0e3) );
geom.set_boundary( 3, Bound(BOUND_NEUMANN,     0.0) );
geom.set_boundary( 4, Bound(BOUND_NEUMANN,     0.0) );
geom.set_boundary( 7, Bound(BOUND_DIRICHLET,   0.0)  );
geom.set_boundary( 8, Bound(BOUND_DIRICHLET, -12.0e3) );
geom.build_mesh();

Next we define the Poisson problem to be solved. For the first round in the Vlasov iteration we need to give a starting guess for the plasma boundary. This is done with set_initial_plasma() with first argument defining the plasma potential (5 volts) and the second argument giving a pointer to a class defining the plasma volume. In case of simple plasma volume at x<0.55 mm we can use a pre-defined convenience class InitialPlasma:

EpotBiCGSTABSolver solver( geom );
InitialPlasma initp( AXIS_X, 0.55e-3 );
solver.set_initial_plasma( 5.0, &initp );

Next we define the needed objects like in the first example:

EpotField epot( geom );
MeshScalarField scharge( geom );
MeshVectorField bfield;
EpotEfield efield( epot );
efield_extrpl_e efldextrpl[6] = { EFIELD_EXTRAPOLATE, EFIELD_EXTRAPOLATE, 
                                  EFIELD_SYMMETRIC_POTENTIAL, EFIELD_EXTRAPOLATE,
                                  EFIELD_EXTRAPOLATE, EFIELD_EXTRAPOLATE };
efield.set_extrapolation( efldextrpl );

ParticleDataBaseCyl pdb( geom );
bool pmirror[6] = { false, false, true, false, false, false };
pdb.set_mirror( pmirror );

After this we are ready for the Vlasov iteration. The first iteration is a special case because of the initial guess for the plasma and therefore after it, the problem had to be redefined to use the non-linear plasma model.

for( size_t i = 0; i < 15; i++ ) {

    if( i == 1 ) {
        double rhoe = pdb.get_rhosum();
        solver.set_pexp_plasma( -rhoe, Te, Up );
    }

    solver.solve( epot, scharge );
    efield.recalculate();

    pdb.clear();
    pdb.add_2d_beam_with_energy( 15000, 600.0, 1.0, 4.0, 
                                 5.0, 0.0, 0.5, 
                                 0.0, 0.0, 
                                 0.0, 0.0015 );
    pdb.iterate_trajectories( scharge, efield, bfield );
}

The particle database calculates the amount of space charge at the definition point and that can be retrieved with get_rhosum(). This value is then fed to the plasma model to define the space charge of background electrons in the plasma. The function set_pexp_plasma() enables the positive exponential plasma model and defines plasma density (first argument), electron temperature (second argument) and plasma potential (third argument). The electric potential is solved using the solver with solver.solve( epot, scharge ). After this the electric field needs to be recalculated with efield.recalculate(). The rest of the Vlasov iteration loops continue as in the first example. Also in the plasma extraction problems it might be necessary to use under-relaxation of space charge field in hard cases.

In this example we invoce the interactive plotter to show the results. You need to provide all the data you want to use in the plotter. Please note that you need to provide the argc and argv parameters to the plotter as the underlying GTK library needs these in initialization.

#ifdef GTK3
    GTKPlotter plotter( argc, argv );
    plotter.set_geometry( &geom );
    plotter.set_epot( &epot );
    plotter.set_scharge( &scharge );
    plotter.set_particledatabase( &pdb );
    plotter.new_geometry_plot_window();
    plotter.run();
#endif

That is it again. The complete source is available here: plasmacyl.cpp and the Makefile: Makefile.

The default screen for the plotter looks something like this:

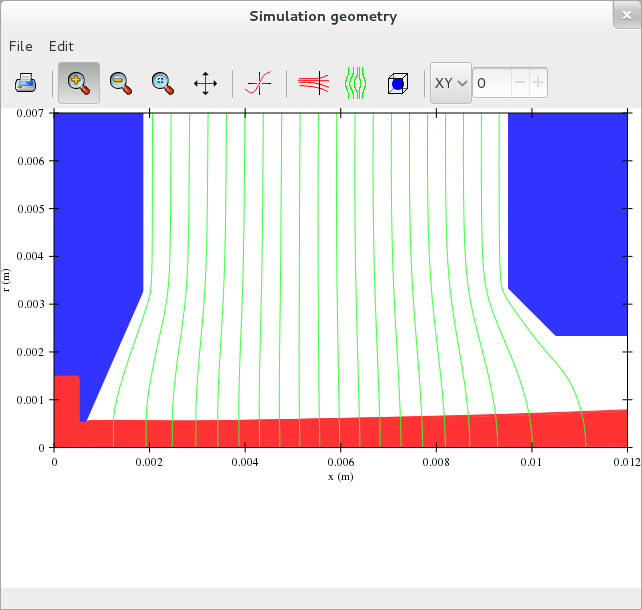
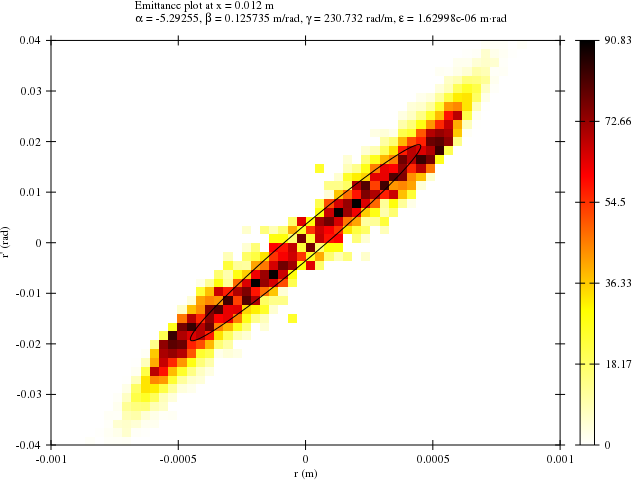
With the interactive tool you can make plots from different view points and you can modify the plotted features using menus. You can also make hardcopies in png, svg, eps and pdf formats. You can plot geometries, emittances, profiles (scatter or colormap style), field values, etc. As an example we have here an emittance plot from this simulation with fitted emittance ellipse: